Roche Glycart AG
https://www.roche.ch/en/sites/schlieren
8952 Schlieren, Wagistrasse 10
+41 43 215 10 00
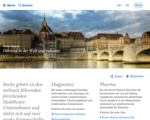
The mission of the Roche Innovation Center Zurich (RICZ) is to be a leader in developing new generations of engineered antibody products with increased efficacy that address unmet clinical needs. The RICZ site is also the Center of Excellence in Cancer Immunotherapy within the Roche Group.
Roche Glycart AG
Wagistrasse 10
8952 Schlieren
73 Ergebnisse für "怎么查酒店开房信息- 查询微信0 25" unter Roche Glycart AG
cobas® 4800システム | ロシュ・ダイアグノスティックス
... 生化学者、学者およびその他の医学研究に関与している人 Your session has expired. Please log in again. cobas® 4800システム 微生物学的検査 ... -496036 コバス 4800システム 検体抽出セット960 960テスト 2~8℃ 518-496043 コバス 4800システム 洗浄試薬 240 240テスト 15~ 25℃ 518-496050 コバス ... 4800システム 洗浄試薬 960 960テスト 15~ 25℃ 518-496067 コバス 4800システム コントロール希釈液 10セット 15~ 25℃ HPV関連 商品コード 製品名 包装 貯法 ...
MagNA Pure 24システム | ロシュ・ダイアグノスティックス
... 100mL - Lysis/Binding Buffer Refill 20mL 100mL 48個 48/50個 40×96個 15~ 25℃ 50個 350(10×35)個 120チューブストリップ 120 ... 全てを見る close 研究試薬 商品コード 製品名 包装 貯法 518-218522 MagNA Pure 24 Total NA Isolation Kit 最大96回 15~ 25℃ 518 ... -218539 MagNA Pure 24 MGP Set 12本 15~ 25℃ 518-221768 MagNA Pure cfNA Buffer Set 最大96回 15~ 25℃ 06640702001 ...
Somagenetix
https://www.wysszurich.ch/projects/somagenetix
8952 Schlieren, Wagistrasse 23
Gene therapy solutions for patients with severe inherited diseases.
Somagenetix
Wagistrasse 23
8952 Schlieren
1 Ergebnisse für "怎么查酒店开房信息- 查询微信0 25" unter Somagenetix
橡インターネットにおける刑法の場所的適用範囲.PDF
... スイスには 25の州に刑事訴訟法が存在する。 11 たとえばインターネット賭博については、賭博台に関する連邦法 12条を参照せよ。 1998年初頭以来、警察庁には(同年の半ばより配置された)2名の捜査官に ... 主義、あるいは世界法主義に従った関係づけ 25も常に 可能であることはいうまでもない。 何と言ってもスイス刑法では、ハードコアポルノの頒布を世界法主義に委ね るといったドイツ刑法 6 条 6 号のよう ... スイスには 25の州に刑事訴訟法が存在する。 11 たとえばインターネット賭博については、賭博台に関する連邦法 12条を参照せよ。 1998年初頭以来、警察庁には(同年の半ばより配置された)2名の捜査官に ... 主義、あるいは世界法主義に従った関係づけ 25も常に 可能であることはいうまでもない。 何と言ってもスイス刑法では、ハードコアポルノの頒布を世界法主義に委ね るといったドイツ刑法 6 条 6 号のよう ...
Standortförderung Kanton Zürich
https://www.zh.ch/de/volkswirtschaftsdirektion/amt-fuer-wirtschaft/standortfoerderung.html
8090 Zürich, Walchestrasse 19
+41 43 259 49 92
standort@vd.zh.ch
The Division of Business and Economic Development supports resident companies, promotes Zurich's innovation capacity by way of connecting the relevant stakeholders in key industries, fosters external economic relations and offers guidance to companies interested in moving to Zurich.
Standortförderung Kanton Zürich
Walchestrasse 19
8090 Zürich
1 Ergebnisse für "怎么查酒店开房信息- 查询微信0 25" unter Standortförderung Kanton Zürich
Elterninformation: Neuzuzug mit schulpflichtigen Kindern - Japanisch
... 、その児童の就学について相談し、疑問点を明らかにするこ とになります。 1 例 誕生日が… 01.08.2019 から 31.07.2020 まで → 入学年度 2024/ 25 01.08.2020 か ... 、その児童の就学について相談し、疑問点を明らかにするこ とになります。 1 例 誕生日が… 01.08.2019 から 31.07.2020 まで → 入学年度 2024/ 25 01.08.2020 か ...
ETH Entrepreneurship
https://ethz.ch/en/industry/entrepreneurship.html
8952 Schlieren, Wagistrasse 18
Excellence in entrepreneurship at ETH Zurich is driven by world-class research and education. It gives rise to groundbreaking new ventures that consolidate Switzerland’s technological leadership. Are you an aspiring entrepreneur seeking to find solutions to global challenges and create a better future for humanity. Or are you just interested in the entrepreneurial ecosystem at ETH Zurich? Browse our websites to find out more or reach out to the Entrepreneurship group, if you have any questions.
ETH Entrepreneurship
Wagistrasse 18
8952 Schlieren
1 Ergebnisse für "怎么查酒店开房信息- 查询微信0 25" unter ETH Entrepreneurship
Numerical Analysis II, Exam End Term Spring 2017
... ∈ [ 0, T ] x( 0) = x0 ∈ R (1.1) with f ∈ C∞ subject to the Lipschitz condition |f(t, x) − f(t, y)| ≤ C|x ... − y| for ∀x, y ∈ R, ∀t ∈ [ 0, T ]. We use the following numerical scheme for (1.1): xk+1 = xk−1 + 2∆tf ... ∈ [ 0, T ] x( 0) = x0 ∈ R (1.1) with f ∈ C∞ subject to the Lipschitz condition |f(t, x) − f(t, y)| ≤ C|x ... − y| for ∀x, y ∈ R, ∀t ∈ [ 0, T ]. We use the following numerical scheme for (1.1): xk+1 = xk−1 + 2∆tf ...